Improvement of optimizing model for coalbed methane pipeline in three-dimensional environment
-
摘要: 在煤层气田的开发过程中, 气体管道的投资占总投资的比例较大, 缩短管道长度可以有效降低投资成本。而在实际设计过程中, 由于两点间的管道连接方式有多种, 因此需要设计者有扎实的设计经验和丰富的现场知识, 极大地增加了工作难度, 为此不少学者提出了三维环境下的管道寻优模型。以现有的管道寻优模型为基础, 以煤层气田开发的实际情况为背景, 对原有的遗传算法提出了改进建议, 通过模拟算例进行验证, 计算结果表明: 改进后的算法能够更有效地解决三维环境下煤层气管道的寻优问题。Abstract: Since investment for gas pipelines shares a big proportion in total investment during coalbed methane development, reducing the length of pipeline can significantly cut down the investment. In practices, the designers need to have rich experiences and knowledge with consideration to multiple ways for connecting two points of pipeline. To reduce the difficulties in practical design, many scholars have proposed the optimizing model for pipeline in three-dimensional environment. On the basis of current optimizing model for pipeline, this paper puts forward improvements of genetic algorithm in the background of coalbed methane field development. By means of case simulation, the verification results demonstrate that the improved algorithm can resolve the problem of optimizing model for coalbed methane pipeline in threedimensional environment more effectively.
-
天然气管道投产前,必须通过水压试验验证管道强度以及管道是否存在泄漏或损坏,水压试验后的大部分剩余水可通过向管道内发送直板清管器、泡沫清管器排出,实现初步脱水[1-2]。然而,一些山区管道地势落差较大,在低洼管段内表面存在较多积水,使输送的天然气在到达下游时含水量超标,无法被用户正常使用,并对生产运行造成较大危害[3-8]:①导致管输天然气质量不合格;②降低压缩机效率,增加压缩机故障率;③低温高压条件下含水天然气易生成固体水合物,造成引压管道、控制阀门及精密过滤器堵塞,影响正常生产[9-13];④液态水与酸性气体混合易生成腐蚀性酸,腐蚀管道内壁[14-15];⑤液态水将聚集在低洼弯管段,降低管道的流通能力,增加输气动力消耗[16-19]。按现有SY/T 4114—2016《天然气管道、液化天然气站(厂)干燥施工技术规范》和CDP-G-OGP-OP-027-2012-1《油气管道清管、试压及干燥技术规定》实施干燥时,常出现干燥不彻底的情况,亟需建立适用于起伏管道的干燥时间预测模型,以指导干燥方案制定及现场施工。
目前天然气长输管道常用干燥方法有干燥剂法、流动气体蒸发法(包括干空气干燥法、氮气干燥法、天然气干燥法)、真空法等。干空气法因其区域局限性小、成本低、干燥效果均匀、安全环保等优势,在实际工程中得到广泛应用。现有干燥模型[20-26]大多在建模过程中作了管内残余水均匀分布的简化假设[27-30],但这种假设不符合起伏管道的实际情况。清管扫水后,起伏管道在地形低洼处存有大量积水,干空气吹扫的时间势必延长,导致现有干燥模型预测值偏差较大。实际干燥过程中管内存水状态未知,无法做到合理规划,继而导致工期不合理及管道内干燥不彻底。基于上述,在分析起伏管道干空气法干燥过程的基础上,建立了干燥时间预测模型,以期指导新建天然气管道的干燥施工与验收,彻底干燥起伏管道,确保管道输送安全及输送天然气的质量合格,实现预期的经济效益和社会效益[31]。
1. 基本概念
1.1 管道特征提取与计算方法
依据目标管段的里程、高程等路由信息,对管道特征点进行提取,简化计算得到管道特征参数。则第n个坡段坡长、坡度及低洼处转角的计算公式分别为:
Ln=√(Yn+1−Yn)2+(Xn+1−Xn)2 (1) tan(an)=|Yn+1−YnXn+1−Xn| (2) βn=180∘−αn−αn−1 (3) 式中:Ln为第n个坡的坡长,m;Xn、Yn分别为第n个坡起点的横坐标、纵坐标;Xn+1、Yn+1分别为第n个坡终点的横坐标、纵坐标;αn为第n个坡的坡度,(°);βn为第n个低洼处的转角度数,(°);其中,上坡时,Yn+1>Yn,下坡时,Yn+1<Yn,低洼处,Yn+1>Yn且Yn-1>Yn。
1.2 管道积液量与接触表面积的函数关系
以干空气干燥速率作为中间参数,由残余水与管壁的几何关系可推导管道内积液量与接触表面积的函数关系。将残余水分为均匀水膜、低洼处残余水两种情况进行分析。
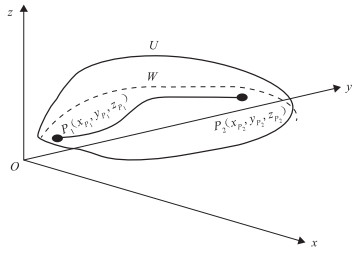
(1)残余水为均匀水膜状态时(图 1),管道积液量的计算表达式为:
Wm=2πRaδ (4) 式中:Wm为管壁均匀水膜状态下积液量,kg;R为管道半径,m;a为积水与管道接触的长度,m;δ为水膜厚度,m。
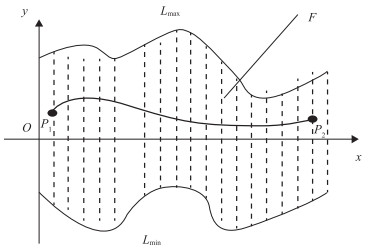
(2)残余水在低洼处聚积时(图 2),管道积液量的计算表达式为:
Wl=916SS′ρ (5) S=R22(θ−sinθ) (6) S′=(R+R′)22(β−sinβ) (7) 式中:Wl为管道低洼处积液量,kg;S为管道与积水接触的径向视图面积,m2;S'为管道与积水接触的轴向视图面积,m2;ρ为水的密度,kg/m3;θ为积水径向视图对应的圆心角;β为管道低洼处转角度数,(°);R'为弯管轴向曲率半径,m。
根据干燥速率的物理意义以及干燥前、后残余水高度的几何关系,可知:
h=h0−Uρt=R−Rcosθ2=R′+R−(R′+R)cosβ2 (8) cosθ2=1−h0−UρtR (9) cosβ2=1−h0−UρtR+R′ (10) 式中:h为积水高度,m;h0为初始积水高度,m;U为干燥速率,kg/(m2·s);t为干燥时间,s。
联立式(5)~式(10),即可得到低洼处管道积液量与积液接触面积的函数关系。
2. 干空气法干燥时间预测模型
天然气管道干空气法干燥过程[32]分为吹扫、封堵吸水两个阶段,若验收不合格,则再干燥吹扫。耦合低洼处管道积液量与表面积的函数关系,分别建立与这两个阶段相对应的干燥模型,通过MATLAB软件求解得到干空气法干燥过程中管道内残余水分布及干空气露点随管长、时间的变化规律,并计算各阶段干燥时间,最终得到总干燥时间。
2.1 吹扫阶段
基于质量守恒定律,建立干空气吹扫阶段的非稳态数学模型。积液质量守恒方程[33]及空气中水蒸气质量守恒方程[25]分别为:
∂W∂t=−πRU (11) Aρ∂C∂t=−M∂C∂x+πDU (12) 式中:W为单位长度管道的积液量,kg/m;A为管道横截面积,m2;C为干空气中水蒸气的质量分数;M为干空气的质量流量,kg/s;x为管道轴向距离变量,m;D为管道内径,m。
对方程赋予初始条件和边界条件,其表达式分别为:
{Wx,0=W0∂W0,t∂x=0 (13) {C0,t=C0Cx,0=Csat (14) 式中:Wx,0为管道x位置处在0时刻吹扫时的单位长度积液量,kg/m;W0为单位长度管道的初始积液量,kg/m;W0,t为管道起点处在t时刻吹扫时的单位长度积液量,kg/m;C0,t为管道起点处在t时刻吹扫时干空气中水蒸气的质量分数;Cx,0为管道x位置处在0时刻吹扫时干空气中水蒸气的质量分数;C0为管道入口处干空气中水蒸气的质量分数;Csat为露点达到饱和时干空气中水蒸气的质量分数。
采用有限差分法对方程进行离散,离散后的控制方程可转化为线性方程组。设定初始积液量、干空气露点及流量、压力等参数,采用高斯-赛德尔迭代方法[34]即可实现干空气吹扫干燥过程迭代计算。当出口气体露点达到-20 ℃时结束连续吹扫并记录干燥时间,转入封堵阶段。
2.2 封堵阶段
吹扫阶段结束后,虽然管壁上的水膜已基本干燥,但低洼弯段处仍有部分残余水存在。为了提高干燥空气的使用效率,将干燥吹扫过程转化为封堵吸水阶段,利用管道中剩余的干燥空气吸收残留的水分,这是一个干空气与水蒸气之间的分子扩散过程。
管道封闭后假设管道内各处压力相同,管道内部温度和压力达到平衡状态,平均压力表示为:
pav=23(pq+p2zpq+pz) (15) 式中:pav为管道内平均压力,Pa;pq、pz分别为吹扫干燥阶段管道的起点压力、终点压力,Pa。
水分子的扩散过程可用Fick第一定律计算[27],其表达式为:
UA=−fABdCAdx (16) 式中:UA为扩散速率,kmol/m2;fAB为组分A到组分B的扩散系数,m2/s;dCAdx为组分A沿管道轴向的浓度梯度,kmol·s/m4。
为迭代求解封堵干燥阶段水分子扩散过程,建立管道内积水和空气中水蒸气的质量守恒方程以及水的蒸发速率与干空气含水量的关系[34-35],其表达式分别为:
∂C′∂t=fAB∂2C′∂x2+2RUm (17) Um=1.57×10−4(1−57.8C′) (18) 式中:C'为封堵阶段干空气中的水蒸气含量,kg/m3;Um为封堵阶段干空气干燥速率,kg/(m2·s)。
随后赋予初始条件和边界条件,其表达式分别为:
C′x,0=φ(x) (19) {∂C′0,t∂x=0∂C′L,t∂x=0 (20) 式中:C'x,0为封堵阶段管道x位置处在0时刻吹扫时干空气中水蒸气的质量分数;C'0,t、C'L,t为封堵阶段管道起点、终点处在t时刻吹扫时干空气中水蒸气的质量分数;L为管道总长度,m;φ(x)为与x有关的函数,为方程的一个特征值。
采用有限体积法对方程进行离散,将控制方程转化为线性方程组,随后采用高斯-赛德尔迭代方法进行干空气含水量的求解。封堵4 h后,检测管道沿线气体露点升高不超过3 ℃且出口露点不超过-20 ℃,则视为管道干燥合格。结束计算并记录封堵阶段干燥时间。
3. 模型验证
3.1 室内实验验证
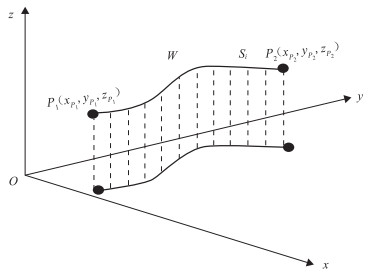
室内搭建连续吹扫实验起伏管道(图 3),特征总长度为40 m,最大坡度为40°,最大坡长为6 m,弯管角度为20°~90°。在管道出口的位置安装露点仪,开展连续吹扫及封堵干燥实验。
连续吹扫实验前向低洼处(图 3注水阀门处)注入1 000 g水,采用4%过盈量的直板清管器扫水,构造管壁均匀水膜的残余水状态。随后通入露点为-40 ℃、流速4 m/s的干空气进行连续吹扫,定时记录出口露点数据,同时采用上述数学模型进行同工况下的连续吹扫干燥预测,将模拟结果与实验值进行对比(图 4)可见,管道完全干燥时间的模拟结果为320 min,实验结果为360 min,模拟结果与实验结果的误差为11%,可认为干空气连续吹扫阶段数学模型较准确可靠。
进行封堵实验前需保证整条管道的管壁干燥,而后向低洼处(图 3注水阀门处)注入200 g水,构造只有低洼处有残余水的状态。随后通入露点为-40 ℃的干空气进行封堵,控制封堵压力为0.06 MPa,定时记录管道出口露点数据,同时采用上述数学模型进行同工况下的封堵干燥预测,将模拟结果与实验值进行对比(图 5)。可见,封堵干燥时间的模拟结果与实验值基本一致,结果吻合较好,可认为干空气封堵阶段数学模型较准确可靠。
3.2 现场工程案例验证
以陕京四线一标段中BA023G+1 554 m-BA030标段管道干燥施工为例,将模型计算的干燥时间与实际干燥时间进行对比。该标段管道内径1 182 mm,长度6 080 m,地温23 ℃,设计露点-20 ℃,现场实际干燥时间120 600 s。用于干燥的干空气露点-40 ℃,流速0.91 m/s。首先通过管道路由数据计算沿线管道起伏特征,从而得到管道内残余水分布状态[36](表 1),全线水膜厚度0.05 mm。利用上述模型模拟吹扫阶段与封堵阶段干燥过程,并计算干燥时间。可知,在吹扫开始132 000 s后,管道符合干燥合格的标准,吹扫结束。与实际施工资料显示的干空气吹扫干燥时间(120 600 s)相比,误差为9.45%,因此,可认为模型计算精度较高。
表 1 陕京四线一标段中BA023G+1 554 m—BA030标段管道特征及低洼处积液量数据表里程/m 高程/m 坡长/m 坡度/(°) 弯管角度/(°) 是否低洼处 积液量/kg 0.0 1 029.56 — — — 否 — 2 98.3 1 059.88 299.84 5.80 — 否 — 686.2 982.06 395.63 -11.34 -17.15 是 25.47 722.3 1 006.98 43.87 34.62 45.96 否 — 2 064.1 874.01 1 348.37 -5.66 -40.28 是 44.87 2 149.9 895.33 88.41 13.95 19.61 否 — 2 447.4 841.70 302.30 -10.22 -24.17 是 142.16 2 748.5 860.54 301.69 3.58 13.80 否 — 2 898.4 830.20 152.94 -11.44 -15.02 是 99.88 3 111.3 841.10 213.18 2.93 14.37 否 — 3 596.2 810.00 485.90 -3.67 -6.6 是 74.27 3 745.3 834.68 151.13 9.40 13.07 否 — 6 080.0 784.68 2 335.24 -1.27 -10.63 否 — 4. 干燥时间影响因素
选取某标段大口径起伏天然气管道(表 2)开展模拟,分析干空气露点、流速及积液量对干燥时间的影响规律。该管道管径为1 016 mm,坡长范围为872~3 770 m;坡度范围为10.96°~48.1°。根据地形起伏特征计算低洼处的积液量分布[36](表 2),全线初始水膜厚度为0.05 mm[23],以此为管道初始积液量。
表 2 某标段大口径起伏天然气管道特征数据表里程/m 高程/m 坡长/m 坡度/(°) 弯管角度/(°) 是否低洼处 积液量/kg 0.0 2 250.31 — — — 否 — 725.1 2 302.72 725.89 4.11 — 否 — 1 776.3 2 240.57 1 051.65 -3.38 -7.49 是 173.74 2 648.2 2 889.00 872.31 48.1 51.48 否 — 11 621.1 2 065.34 8 973.32 -5.27 53.37 是 742.41 15 391.4 2 782.51 3 770.56 10.96 16.23 否 — 21 006.3 1 967.23 5 695.79 -8.23 -19.19 是 382.621 23 024.2 2 649.46 1 938.63 20.6 28.83 否 — 25 196.4 2 275.12 2 172.21 -9.9 -30.52 是 326.86 26 851.1 2 391.00 1 655.35 4.02 13.93 否 — 27 230.3 2 245.54 379.21 -22.66 -26.68 是 267.82 28 583.3 2 888.37 1 353.00 28.37 51.03 否 — 32 000.0 2 210.75 2 417.87 -16.26 -39.00 否 — 4.1 干空气露点及流速
利用上述模型计算不同干空气露点(-30℃、-40 ℃、-50 ℃、-60 ℃)及流速(4 m/s、5 m/s、6 m/s、7 m/s、8 m/s)下管道进行干空气法吹扫的干燥时间,从而获得露点及管道单位长度积液量随管长的变化关系,以便分析最优的干空气技术指标。
通过对不同流速与露点交叉工况的模拟,得到不同干空气露点、流速下管道的干燥时间(图 6)。可见,在该管道条件下,不同的干空气流速下露点达到-40 ℃之后,继续降低露点对缩短管道干燥时间的效果不明显,说明露点不宜低于-40 ℃。不同的干空气露点下流速达到6 m/s后,继续增大流速对缩短干燥时间的影响不大,因此干空气流速不宜高于6 m/s。
4.2 沿线积液量
采用上述模型模拟得到不同干燥时刻管道单位长度积液量随里程的变化曲线(图 7)及干空气含水量随里程的变化曲线(图 8)。可见,管道低洼处残余水(曲线尖峰部分)与管壁水膜(横坐标轴上方平缓部分)均呈现由前至后的干燥规律;两者同时存在时,相比低洼处残余水,管壁水膜先被干燥,如125.73 h时,位于11.6 km的低洼处管壁水膜已经被干燥,而此时管道内还存在残余水。结合图 8可知,当管道出口处干空气露点达到-20 ℃时,管道25 km、27 km处的低洼处仍有残余水,说明针对现场多起伏的天然气管道而言,如何快速干燥低洼处残余水至关重要。
5. 结论
在考虑低洼处残余水及管壁水膜同时存在的情况下,结合干燥施工标准,建立了起伏天然气管道干空气法干燥时间预测模型,通过模拟值与室内实验值的对比验证了模型的准确性。该模型可预测干空气法进行天然气管道吹扫的干燥时间,实时监测沿线露点及残余水分布的变化规律。起伏天然气管道干燥过程中干空气露点不宜低于-40 ℃,流速不宜高于6 m/s。对于起伏天然气管道而言,低洼处残余水较多,因此管壁水膜先干燥,低洼处残余水后干燥。在干燥作业过程中除了需要关注标准要求的相关指标之外,还要确保低洼处残余水干燥彻底。后续可继续研究干空气连续吹扫过程中通泡沫清管器对干燥时间的影响,提高模型准确度,以期更好指导起伏天然气管道干燥方案设计与施工。
-
[1] 冉戎. 基于GIS的道路自动化选线方法研究[D]. 重庆: 重庆大学, 2006: 40-43. RAN R. Methods of selecting road route automatically based on GIS[D]. Chongqing: Chongqing University, 2006: 40-43.
[2] 黄樟灿, 陈思多, 康立山, 等. 基于模拟退火算法的曲面最短路径求解[J]. 武汉大学学报, 2000, 46(6): 273 -276. https://www.cnki.com.cn/Article/CJFDTOTAL-WHDY200003003.htm HUANG Z C, CHEN S D, KANG L S, et al. Solving the shortest path on curved surface based on simulated annealing algorithm[J]. Journal of Wuhan University, 2000, 46(6): 273-276. https://www.cnki.com.cn/Article/CJFDTOTAL-WHDY200003003.htm
[3] 吴晓涛, 孙增圻. 用遗传算法进行路径规划[J]. 清华大学学报, 1995, 35(5): 14-19. https://www.cnki.com.cn/Article/CJFDTOTAL-QHXB505.003.htm WU X T, SUN Z Q. Using genetic algorithm for path planning[J]. Journal of Tsinghua University, 1995, 35(5): 14-19. https://www.cnki.com.cn/Article/CJFDTOTAL-QHXB505.003.htm
[4] 陈思多, 黄樟灿. 坡度约束下曲面最短路径算法[J]. 武汉汽车工业大学学报, 2000, 22(1): 84-87. https://www.cnki.com.cn/Article/CJFDTOTAL-WHQC200001021.htm CHEN S D, HUANG Z C. Algorithm of the shortest path on curved surface under slope constraints[J]. Journal of Wuhan University of Technology, 2000, 22(1): 84-87. https://www.cnki.com.cn/Article/CJFDTOTAL-WHQC200001021.htm
[5] 刘春林, 何建敏, 盛昭瀚. 给定限制条件下最小风险路径的选取算法[J]. 系统工程学报, 1999, 14(3): 221-226. https://www.cnki.com.cn/Article/CJFDTOTAL-XTGC199903003.htm LIU C L, HE J M, SHENG Z H. An algorithm to select the minimum risk path by a given deadline[J]. Journal of System Engineering, 1999, 14(3): 221-226. https://www.cnki.com.cn/Article/CJFDTOTAL-XTGC199903003.htm
[6] 陈雪冬, 杨武年, 罗虎. 基于栅格数据道路选线模型算法的应用研究[J]. 公路, 2004(5): 6-9. https://www.cnki.com.cn/Article/CJFDTOTAL-GLGL200405001.htm CHEN X D, YANG W N, LUO H. Research on algorithm of road routing model based on grid data[J]. Highway, 2004(5): 6-9. https://www.cnki.com.cn/Article/CJFDTOTAL-GLGL200405001.htm
[7] 蒋玉明. 快速求取自由曲面上两点的最短路径算法[J]. 计算机辅助设计与图形学学报, 1994, 6(1): 28-32. https://www.cnki.com.cn/Article/CJFDTOTAL-JSJF401.004.htm JIANG Y M. An algorithm for fast finding the shortest path between two points on free-form surface[J]. Journal of ComputerAided Design & Computer Graphics, 1994, 6(1): 28-32. https://www.cnki.com.cn/Article/CJFDTOTAL-JSJF401.004.htm
[8] OLORUNNIWO F O. A methodology for optimal design and capacity expansion planning of natural gas transmission networks[D]. Austin: University of Texas at Austin, 1981: 181-183.
[9] HANSEN C T, MADSEN K, NILSEN H B. Optimization of large networks[J]. Mathematical Programming, 1991(52): 41-45.
[10] 张启阳, 史培玉, 李玉星. 基于遗传算法的油气混输管网参数优化[J]. 石油规划设计, 2004, 15(3): 25-28. https://www.cnki.com.cn/Article/CJFDTOTAL-SYGH200403008.htm ZHANG Q Y, SHI P Y, LI Y X. Optimization of parameters for combined oil and gas pipelining networks based on genetic algorithm[J]. Petroleum Planning & Engineering, 2004, 15(3): 25-28. https://www.cnki.com.cn/Article/CJFDTOTAL-SYGH200403008.htm
[11] 娄红洋, 张宏波, 许铁红, 等. 油气混输管网参数优化研究[J]. 河南石油, 2006, 20(2): 87-88. https://www.cnki.com.cn/Article/CJFDTOTAL-SYHN200602033.htm LOU H Y, ZHANG H B, XU T H, et al. Study on parameter optimization of combined network of pipeline[J]. Henan Petroleum, 2006, 20(2): 87-88. https://www.cnki.com.cn/Article/CJFDTOTAL-SYHN200602033.htm
[12] 李卫华, 李长俊. 基于遗传算法的天然气集输管网参数优化设计[J]. 天然气工业, 2005, 25(2): 158-160. https://www.cnki.com.cn/Article/CJFDTOTAL-TRQG20050201F.htm LI W H, LI C J. Parameter-optimized design of gas gathering and transmission system by heredity solution[J]. Natural Gas Industry, 2005, 25(2): 158-160. https://www.cnki.com.cn/Article/CJFDTOTAL-TRQG20050201F.htm
[13] GOLDBERG D E, KOU C H. Genetic algorithms in pipeline optimization[J]. Journal of Computing in Civil Engineering, 1987, 1(2): 128-141.





 下载:
下载: